jueves, 31 de marzo de 2016

Explicación de versores (clase)

La descomposición de un vector unitario y sus componentes i y j. ¿Que son los vectores i y j? son vectores cuya magnitud es de una unidad. Es decir que la magnitud del vector i y la magnitud del vector j es igual a 1 cada uno. Para descomponer un vector en sus vectores unitarios i y j , el vector debe estar ubicado en un plano cartesiano.

viernes, 25 de marzo de 2016

Carga eléctrica

Interpretación de las ecuaciones de Maxwell

Fotos tomadas en clase

lunes, 14 de marzo de 2016

ELECTRIZACIÓN Cuando a un cuerpo se le dota de propiedades eléctricas, es decir, adquiere cargas eléctricas, se dice que ha sido electrizado.

La electrización es uno de los fenómenos que estudia la electrostática.

Para explicar como se origina la electricidad estática, hemos de considerar que la materia está hecha de átomos, y los átomos de partículas cargadas, un núcleo rodeado de una nube de electrones. Normalmente, la materia es neutra (no electrizada), tiene el mismo número des cargas positivas y negativas.

Algunos átomos tienen más facilidad para perder sus electrones que otros. Si un material tiende a perder algunos de sus electrones cuando entra en contacto con otro, se dice que es más positivo en la serie Triboeléctrica. Si un material tiende a capturar electrones cuando entra en contacto con otro material, dicho material es más negativo en la serie triboeléctrica.

Un ejemplo de materiales ordenados de más positivo a más negativa es el siguiente:

Piel de conejo, vidrio, pelo humano, nylon, lana, seda, papel, algodón, madera, ámbar, polyester, poliuretano, vinilo (PVC), teflón.

El vidrio frotado con seda provoca una separación de las cargas por que ambos materiales ocupan posiciones distintas en la serie triboeléctrica, lo mismo se puede decir del ámbar y del vidrio. Cuando dos materiales no conductores entran en contacto uno de los materiales puede capturar electrones del otro material. La cantidad de carga depende de la naturaleza de los materiales (de su separación en la serie triboeléctrica), y del área de la superficie que entra en contacto. Otro de los factores que intervienen es el estado de las superficies, si son lisas o rugosas (entonces, la superficie de contacto es pequeña). La humedad o impurezas que contengan las superficies proporcionan un camino para que se recombinen las cargas. La presencia de impurezas en el aire tiene el mismo efecto que la humedad

PROCESOS PARA CARGAR UN SISTEMA

Electrización por frotamiento
La electrización por frotamiento se explica del siguiente modo. Por efecto de la fricción, los electrones externos de los átomos del paño de lana son liberados y cedidos a la barra de ámbar, con lo cual ésta queda cargada negativamente y aquél positivamente. En términos análogos puede explicarse la electrización del vidrio por la seda. En cualquiera de estos fenómenos se pierden o se ganan electrones, pero el número de electrones cedidos por uno de los cuerpos en contacto es igual al número de electrones aceptado por el otro, de ahí que en conjunto no hay producción ni destrucción de carga eléctrica. Esta es la explicación, desde la teoría atómica, del principio de conservación de la carga eléctrica formulado por Franklin con anterioridad a dicha teoría sobre la base de observaciones sencillas

Electrización por contacto
La electrización por contacto es considerada como la consecuencia de un flujo de cargas negativas de un cuerpo a otro. Si el cuerpo cargado es positivo es porque sus correspondientes átomos poseen un defecto de electrones, que se verá en parte compensado por la aportación del cuerpo neutro cuando ambos entran en contacto, El resultado final es que el cuerpo cargado se hace menos positivo y el neutro adquiere carga eléctrica positiva. Aun cuando en realidad se hayan transferido electrones del cuerpo neutro al cargado positivamente, todo sucede como si el segundo hubiese cedido parte de su carga positiva al primero. En el caso de que el cuerpo cargado inicialmente sea negativo, la transferencia de carga negativa de uno a otro corresponde, en este caso, a una cesión de electrones

Electrización por inducción
La electrización por influencia o inducción es un efecto de las fuerzas eléctricas. Debido a que éstas se ejercen a distancia, un cuerpo cargado positivamente en las proximidades de otro neutro atraerá hacia sí a las cargas negativas, con lo que la región próxima queda cargada negativamente. Si el cuerpo cargado es negativo entonces el efecto de repulsión sobre los electrones atómicos convertirá esa zona en positiva. En ambos casos, la separación de cargas inducida por las fuerzas eléctricas es transitoria y desaparece cuando el agente responsable se aleja suficientemente del cuerpo neutro.

Electrizacion por polarización

Cuando se acerca un cuerpo cargado a un no conductor produce un desplazamiento de los electrones muy pequeño (menor que el diámetro atómico). Haciendo que las moléculas de este cuerpo adquieran una “POLARIZACION”. No hay movimiento de cargas en distancias grandes como sucede cuando se desplazan en un conductor. El reordenamiento de las cargas en un aislador debido a la presencia de otro cuerpo cargado se denomina Polarización.

Conductores, aisladores y semiconductores
Cuando un cuerpo neutro es electrizado, sus cargas eléctricas, bajo la acción de las fuerzas correspondientes, se redistribuyen hasta alcanzar una situación de equilibrio. Algunos cuerpos, sin embargo, ponen muchas dificultades a este movimiento de las cargas eléctricas por su interior y sólo permanece cargado el lugar en donde se depositó la carga neta. Otros, por el contrario, facilitan tal redistribución de modo que la electricidad afecta finalmente a todo el cuerpo. Los primeros se denominan aisladores y los segundos conductores.

Esta diferencia de comportamiento de las sustancias respecto del desplazamiento de las cargas en su interior depende de su naturaleza íntima. Así, los átomos de las sustancias conductoras poseen electrones externos muy débilmente ligados al núcleo en un estado de semilibertad que les otorga una gran movilidad, tal es el caso de los metales. En las sustancias aisladoras, sin embargo, los núcleos atómicos retienen con fuerza todos sus electrones, lo que hace que su movilidad sea escasa.

Entre los buenos conductores y los aisladores existe una gran variedad de situaciones intermedias. Es de destacar entre ellas la de los materiales semiconductores por su importancia en la fabricación de dispositivos electrónicos que son la base de la actual revolución tecnológica. En condiciones ordinarias se comportan como malos conductores, pero desde un punto de vista físico su interés radica en que se pueden alterar sus propiedades conductoras con cierta facilidad, ya sea mediante pequeños cambios en su composición, ya sea sometiéndolos a condiciones especiales, como elevada temperatura o intensa iluminación.

jueves, 10 de marzo de 2016

ECUACIONES DE MAXWELL

La Ecuaciones de Maxwell surgen de la teoría electromagnética y son el resumen esta teoría desde un punto de vista macroscópico.Y son, por tanto, un total de ocho ecuaciones escalares (tres para cada uno de los rotacionales de los campos eléctrico y magnético y una para las divergencias).

Parámetros presentes

Los parámetros que intervienen en la formulación de las ecuaciones de Maxwell son los siguientes:

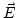$\vec{E}$ - Campo eléctrico existente en el espacio, creado por las cargas.
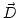$\vec{D}$ - Campo dieléctrico que resume los efectos eléctricos de la materia.
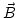$\vec{B}$ - Campo magnético existente en el espacio, creado por las corrientes.
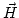$\vec{H}$ - Campo magnético que resume los efectos magnéticos de la materia.
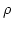$\rho$ - Densidad de cargas existentes en el espacio.
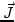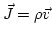$\vec{J}$ - Densidad de corriente, mide el flujo de cargas por unidad de tiempo y superfície y es igual a $\vec{J}=\rho\vec{v}$ .
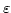$\varepsilon$ - Permitividad eléctrica, característica de los materiales dieléctricos.
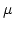$\mu$ - Permeabilidad magnética, característica de los materiales paramagnéticos.
Significado físico
Cuando Maxwell resumió la teoría electromagnética de su época en sus ecuaciones escribió las siguientes ecuaciones:

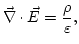
$\displaystyle \div{E}=\frac{\rho}{\varepsilon},$

que no es nada más que la ley de Gauss, que se reduce a la ley de Coulomb para cargas puntuales.

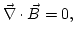
$\displaystyle \div{B}=0,$

que no tiene nombre y expresa la inexistencia de monopolos magnéticos en la naturaleza, es decir, esta es la explicación de que al romper un imán obtengamos dos imanes, y no dos medio-imanes.

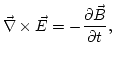$\displaystyle \vec{\nabla}\times\vec{E}=-\frac{\partial \vec{B}}{\partial t},$ que es la expresión diferencial de la ley de Faraday.

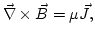
$\displaystyle \vec{\nabla}\times\vec{B}=\mu\vec{J},$

que es la ley de Ampère. Sin embargo encontró que esta última ecuación, juntamente con la ley de Faraday conducían a un resultado que violaba el principio de conservación de la carga, con lo cual decidió modificarla para que no violase este principio dándole la forma

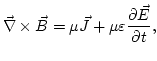
$\displaystyle \vec{\nabla}\times\vec{B}=\mu\vec{J}+\mu\varepsilon\frac{\partial \vec{E}}{\partial t},$

que ahora se conoce como ley de Ampère modificada. El término introducido recibe el nombre de corriente de desplazamiento.Sin embargo estas ocho ecuaciones no son suficientes para resumir todo el conocimiento de la electrodinámica clásica, nos hace falta una ecuación más, esa es la expresión de la fuerza de Lorentz:

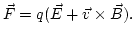
$\displaystyle \vec{F}=q(\vec{E}+\vec{v}\times\vec{B}).$

Electrostática y magnetostática
Cuando consideramos que los campos eléctrico y magnético no dependen del tiempo las ecuaciones de Maxwell se nos quedan en:

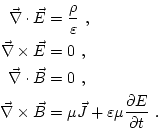
$\begin{equation*}\begin{aligned} \div{E}&=\frac{\rho}{\varepsilon}\ ,\\ \vec{... ...psilon\mu\frac{\partial E}{\partial t}\ .\nonumber \end{aligned}\e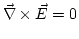nd{equation*}$

De $\vec{\nabla}\times\vec{E}=0$ sacamos que el campo eléctrico se deriva del gradiente de un potencial, es decir, 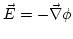$\vec{E}=-\vec{\nabla}\phi$ , como se desprende de la ley de Coulomb.De 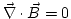$\div{B}=0$ deducimos que el campo magnético es el rotacional de un potencial vector, es decir, 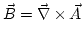$\vec{B}=\vec{\nabla}\times\vec{A}$ , obteniendo el mismo resultado que a partir de la ley de Biot-Savart.

4.3 Ecuaciones de Maxwell en el vacío
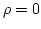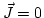Cuando estamos en el vacío podemos suponer que no existen fuentes (es decir, que $\rho=0$ y $\vec{J}=0$ ) y las ecuaciones de Maxwell nos quedan de la forma:

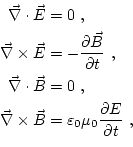
$\begin{equation*}\begin{aligned} \div{E}&=0\ ,\\ \vec{\nabla}\times\vec{E}&=-... ...0}\mu_{0}\frac{\partial E}{\partial t}\ ,\nonumber \end{aligned}\end{equation*}$

En este caso se puede demostrar que tanto el campo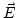 $\vec{E}$ como el campo 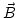$\vec{B}$ toman la forma de una ecuación de ondas con una velocidad 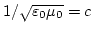$1/\sqrt{\varepsilon_{0}\mu_{0}}=c$ igual a la velocidad de la luz, de donde Maxwell extrajo la hipótesis de que la luz no eran más que ondas electromagnéticas propagándose en el vacío, hipótesis verificada esperimentalmente por Hertz algunos años después de la muerte de Maxwell.A partir de estas cuatro ecuaciones (dos de ellas vectoriales, con lo que en realidad son ocho ecuaciones escalares) se deduce la óptica electromagnética.
http://www.lawebdefisica.com/dicc/maxwell/